[JAVA数据结构]Java排序（七大排序 + 动图代码解析）

排序有很多种，一般以主流升序或者降序为主（不包含特殊的排序序列）[这里讲解都是升序且是整形，其他类型以此类推，改个符号和比较方法就好]

排序在很多场景下特别场景，例如淘宝的各种排序列表，高效的排序在这里显得尤为重要，所以在讲解排序时，会结合复杂度的分析

对于链表的排序我建议用归并

下列这个图只是思想上的分类罢了

排序是否稳定：在于相同的元素是否被交换了先后位置

七大排序之中，只有《直接插入排序》《冒泡排序》《归并排序》是稳定的。

1.插入排序

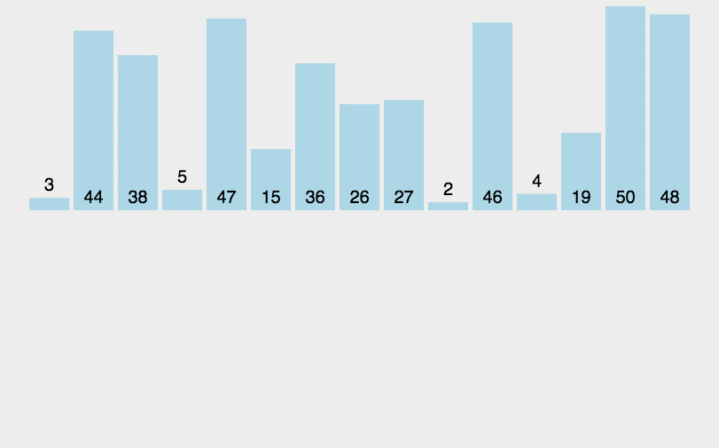
大家可以多看几次动图，这样理解起来会更好

没错，如你所见，插入排序就是，下标从左往右走，没次将对应下标的元素往前插入到合适的位置（不一定是最终位置），然后大于他的就往后挪，（挪的方法一定是从尾巴往后，这样就不会影响其他值）

始终都有个位置留给这个值，不管是否需要挪动/***插入排序*@paramarr*///时间O(N^2)最好的情况是O(N)数据接近有序，建议插入排序//空间O(1)//是稳定的，稳定是可以实现为不稳定//但是不稳定是不可实现为稳定的publicstaticvoidinsertSort(int[]arr){arr=Arrays.copyOf(arr,arr.length);//这一步只是堆数组进行拷贝（引用类型记得设计为深拷贝哦！）//目的是为了不改变原数组，方便多组测试for(inti=1;i=0&&arr[j]>tmp;j--){arr[j+1]=arr[j];}//插入空地里arr[j+1]=tmp;}//可以在这里sout打印一下}

2.希尔排序

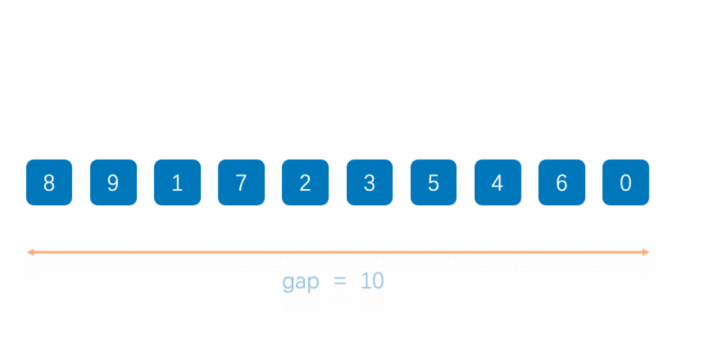
大家可以多看几次动图，这样理解起来会更好，并且一定要结合插入排序的思想！

总体来说，这个排序在插入排序的基础上，增加了“随机性”-–>就是让后面排在前面的数据，有更大的机会提前排好，减少极端条件下，数据被挪动很多次！但是也因此失去了[稳定性]

这里有一个很重要的变量[gap，间隔]，每次间隔都会变小，其实插入排序的间隔是1，这里希尔排序的间隔从大到小，实际上就是"跳着比较，跳着挪",当gap==1时，退化成希尔排序，但是希尔排序，越有序越快！

/***希尔排序*时间复杂度O(N^1.3)-O(N^1.5)，至今还未能精确算出！*空间复杂度O(1)*[不稳定]排序*@paramarr*///一趟一趟的排！publicstaticvoidshellSort(int[]arr){arr=Arrays.copyOf(arr,arr.length);intgap=arr.length/2;while(gap>=1){shell(arr,gap);gap/=2;}}//一趟希尔排序的希尔方法-----》无非就是插入排序的1-->gappublicstaticvoidshell(int[]arr,intgap){for(inti=gap;i=0){if(arr[j]>tmp){arr[j+gap]=arr[j];}else{break;}j-=gap;}arr[j+gap]=tmp;}}

3.选择排序

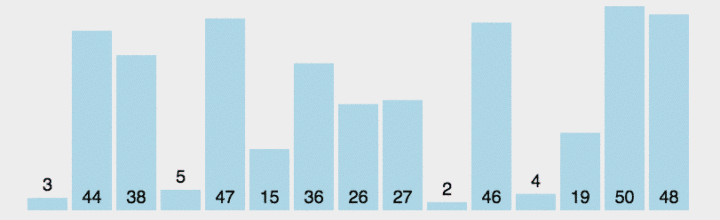
大家可以多看几次动图，这样理解起来会更好

由于选择排序有交换的情节，在一趟选择,如果一个元素比当前元素小,而**该小的元素又出现在一个和当前元素相等的元素后面,那么交换后稳定性就被破坏了。

不难看出，每趟排序，都在往后（对应局部空间，不包含已排好部分）选择最小值进行交换，每次都能确定一个元素的最终位置

/***选择排序*时间复杂度O(N^2)*空间复杂度O(1)*[不稳定]*@paramarr*/publicstaticvoidselectSort1(int[]arr){arr=Arrays.copyOf(arr,arr.length);for(inti=0;iarr[j]){minIndex=j;}}if(i!=minIndex){inttmp=arr[minIndex];arr[minIndex]=arr[i];arr[i]=tmp;}}}

4.堆排序

一定要学习堆知识后再学习这个排序！

用到的原理无非就是，建立大根堆，堆顶元素删除时会被放在[末尾]，就是说最大元素每次都被插都后面，确定最终位置！

由于堆对应的结构是完全二叉树，所以这种排序效率上不会因为数据怎么样而变化很大。

/***堆排序*时间复杂度为O(N*log2N)N*logN+N---->N*logN(取最高阶)*空间复杂度为O(1);*[不稳定]（排在前面的相同元素会更快的被查到后面）*@paramarr*///一趟一趟排publicstaticvoidheapSort(int[]arr){arr=Arrays.copyOf(arr,arr.length);//方便测试，这条语句去掉就是O(1)createHeap(arr);for(intend=arr.length-1;end>=0;end--){//将堆顶与[末尾]交换，inttmp=arr[0];arr[0]=arr[end];arr[end]=tmp;//并且保证刚才那个之前的那一部分仍是大根堆shiftDown(arr,0,end-1);}}//每次都要向下调整（向下调整一次就好，向上可能要很多次，这里参考堆的知识），保证还是大根堆！privatestaticvoidshiftDown(int[]arr,intparent,intlen){intchild=2*parent+1;while(childarr[child]){child++;}if(arr[child]>arr[parent]){inttmp=arr[child];arr[child]=arr[parent];arr[parent]=tmp;parent=child;child=2*parent+1;}else{break;}}}//建立大根堆方法！向下调整的构造法，节省大量时间！privatestaticvoidcreateHeap(int[]arr){for(inti=(arr.length-2)/2;i>=0;i--){shiftDown(arr,i,arr.length-1);}}

5.冒泡排序

大家可以多看几次动图，这样理解起来会更好

不难看出，每趟排序都能将最大的值传到最后(确定最终位置)，一旦判断到相邻元素左>右就会交换

每次交换都纠正了两个元素的宏观相对位置

一趟排序确定一个，那么那一个就不需要参与下一趟排序

最后一趟排序只有一个元素，可以忽略

确定有序就结束

/***冒泡排序*时间复杂度（不考虑优化）O(N^2)*空间复杂度O(1)**[稳定]*@paramarr*/publicstaticvoidbubbleSort(int[]arr){arr=Arrays.copyOf(arr,arr.length);for(inti=0;iarr[j]){flag=false;inttmp=arr[j-1];arr[j-1]=arr[j];arr[j]=tmp;}}if(flag){return;//--->排好就收！}}}

6.快速排序

（了解，不了解都无所谓）如果你学习到了二叉搜索树，不难看出他在逻辑上是数组型的二叉搜索树

重点在于一个变量[pivot，基准值]----这个值作为分界点，左边都比它小，右边都比它大

我们需要挪动pivot，在这个过程中解决左右值的问题

6.1基准的确定

对于基准值，一味的用第一个元素，若遇到极端情况下（排好的正序or逆序），排序速度会很慢，因为这种情况下基准值确定位置后，仅仅往后移了一位，相当于每趟确定左值为最小（或者右值最大），相当于退化成冒泡排序了。

上面这种情况下，甚至会栈溢出！因为一些方法栈帧没有销毁，又有新的栈帧了。

下面是优化方案：三值取中法

这样可以保证基准确定位置后，趋中

确认基准值之后，应该将其放在[头]，这样左右下标就可以走遍整个序列啦

privatestaticintfindMid(int[]arr,intleft,intright){intmid=(left+right)>>>1;if(arr[left]arr[right]){returnright;}else{returnmid;}}else{if(arr[mid]>arr[right]){returnright;}elseif(arr[mid]

6.2临近末尾

快速排序一般用于排序海量数据，排序很多趟之后，其实一段序列基本有序了，所以可以采取插入排序可以增加速率

思想：快速排序可以快速排序很乱的序列（不是逆序，而是乱），再用插入排序解决序列较有序的序列，大大提高效率

下面是优化方案：

privatestaticfinalintQUIT_METHOD=50;//优化2---->减少后面的递归，因为在很多次的找pivot后，其实会变得很有序，那么这个时候用插入排序会很快解决问题privatestaticvoidinsertLittleSort(intarr[],intleft,intright){for(inti=left+1;i=0&&arr[j]>tmp;j--){arr[j+1]=arr[j];}arr[j+1]=tmp;}}

6.3三种基准调整方法：

6.3.1挖坑法：

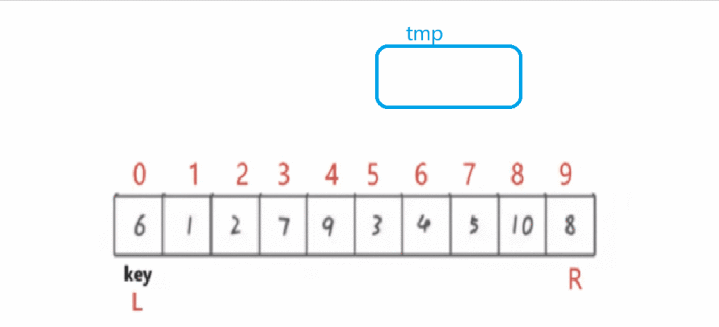
多看几次动图！这种方法比较随意，这里在首元素的[坑]最先填上，然后替换的原位置成为新的坑

//挖坑法privatestaticintpartition1(int[]arr,intleft,intright){inttmp=arr[left];while(left=tmp){//等号两个都不取的话，那么就会死循环right--;}arr[left]=arr[right];//left为刚才的坑while(left

6.3.2Hoare法（最初）

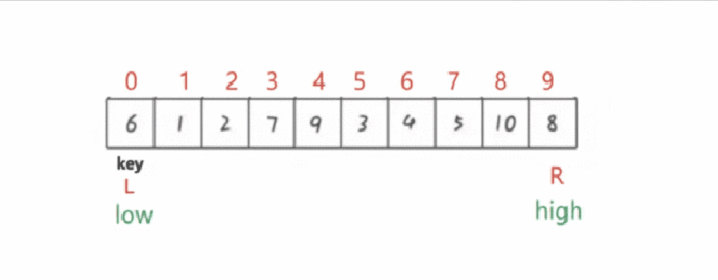
多看几次动图！这方法一开始基准最后再与相遇时下标对应的元素交换

//Hoare法privatestaticintpartition2(int[]arr,intleft,intright){intindex=left;while(left=arr[index]){right--;}while(left

6.3.3前后下标指针法（了解即可）

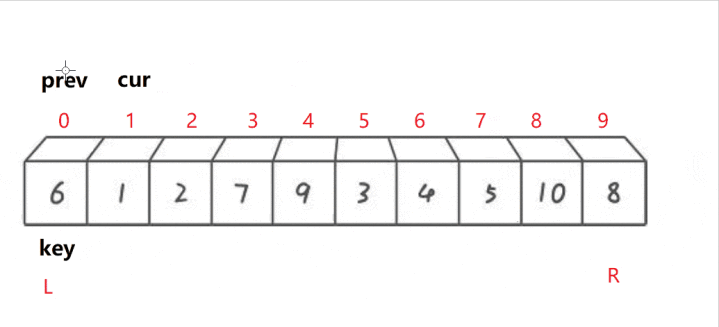
多看几次动图！这种方法保证了prev后面不存在小于基准值的元素！

//前后指针法privatestaticintpartition3(int[]arr,intleft,intright){intprev=left;intcur=left+1;while(cur

6.4递归法代码实现

这里展示的是挖坑法，只需要将方法名改一下就OK了！

要结合递归思想，左边排完看成整体，右边排完看成整体

别忘了递归出口，这里优化后是交给插入排序

/***快速排序*时间复杂度:O(N*log2N)(最好)O(N^2)（最坏，正序or逆序）（越有序越慢）*空间复杂度:O(log2N)(最好)O(N)(最坏)*[不稳定]----->因为相同值在交换到对立位置是有先后的，如果不是基准值相同，则很大可能不稳定*并且靠前的相同值会被换到上一个后面的位置*@paramarr*/publicstaticvoidquickSort1(int[]arr){arr=Arrays.copyOf(arr,arr.length);quick1(arr,0,arr.length-1);}privatestaticvoidquick1(int[]arr,intleft,intright){if(left>=right){return;}intindex=findMid(arr,left,right);if(right-left+1

6.5非递归实现(了解)

6.5.1栈模拟递归前序遍历

这里一些基础方法与递归使用的是一样的！

栈的先进后出，可以很好的模拟递归的“归”

publicstaticvoidquickSortNormal1(int[]arr){arr=Arrays.copyOf(arr,arr.length);//栈模拟递归Dequestack=newLinkedList;//也可以用队列模拟层序遍历，这就不是往模拟递归的方向走了//思路是一层完了之后再下一层，直到结束intleft=0;intright=arr.length-1;do{intindex=findMid(arr,left,right);{//因为我们都是默认从第一个做基准值，所以我们只需要与第一个换一下位置就好了，并且我们是在两端向中的，所以这样最规范最全面合适inttmp=arr[index];arr[index]=arr[left];arr[left]=tmp;}intpivot=partition3(arr,left,right);if(pivot-left>=1){stack.push(left);stack.push(pivot-1);}if(right-pivot>=1){stack.push(pivot+1);stack.push(right);}if(!stack.isEmpty){right=stack.pop;left=stack.pop;}else{break;}}while(true);}

6.5.2队列模拟递归层序遍历

队列的先进先出，按照应有的顺序，一层一层的来。不像栈那种模拟深度优先(到底在归即为深度优先)

publicstaticvoidquickSortNormal2(int[]arr){arr=Arrays.copyOf(arr,arr.length);//队列模拟递归Queuequeue=newLinkedList;intleft=0;intright=arr.length-1;do{intindex=findMid(arr,left,right);{//因为我们都是默认从第一个做基准值，所以我们只需要与第一个换一下位置就好了，并且我们是在两端向中的，所以这样最规范最全面合适inttmp=arr[index];arr[index]=arr[left];arr[left]=tmp;}intpivot=partition3(arr,left,right);if(pivot-left>=1){queue.offer(left);queue.offer(pivot-1);}if(right-pivot>=1){queue.offer(pivot+1);queue.offer(right);}if(!queue.isEmpty){left=queue.poll;right=queue.poll;}else{break;}}while(true);}

7.归并排序

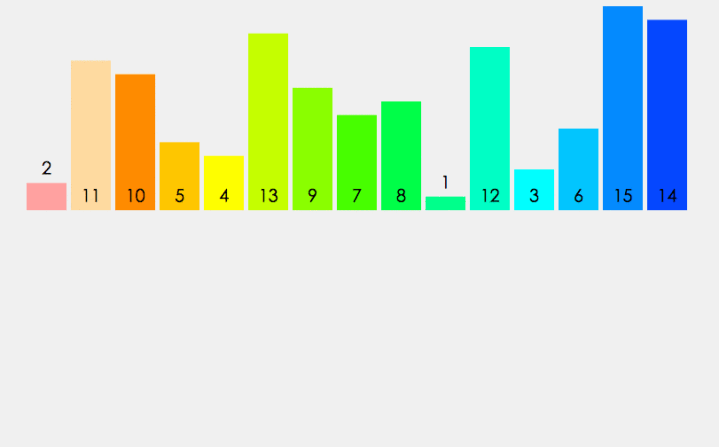
大家可以多看几次动图，这样理解起来会更好

分成很多小份排，然后逐渐变大份，（递归思想）

多用于多海量文件排序

7.1递归实现

/***归并排序*时间复杂度O(N*logN)*空间复杂度O(N)*[稳定的]*@paramarr*/publicstaticvoidmergeSort(int[]arr){arr=Arrays.copyOf(arr,arr.length);mergeSorter(arr,0,arr.length-1);}privatestaticvoidmergeSorter(int[]arr,intleft,intright){if(left>=right){return;}intmid=(left+right)>>>1;mergeSorter(arr,left,mid);mergeSorter(arr,mid+1,right);merge(arr,left,right,mid);}//将序列划分为两部分，并且两部分是有序的，那么只需要合并有序序列就好privatestaticvoidmerge(int[]arr,intleft,intright,intmid){intleft1=left;intleft2=mid+1;intlen=right-left+1;int[]tmp=newint[len];intnum=0;while(left1

7.2非递归实现

重点就在于[gap]从小到大，之间按照原理来的

/***非递归归并排序*@paramarr*/publicstaticvoidmergeSortNormal(int[]arr){arr=Arrays.copyOf(arr,arr.length);//这不需要stack模拟递归，直接根据原理就好intgap=1;while(gap

7.3归并排序链表（普通的排序可能会超时！）

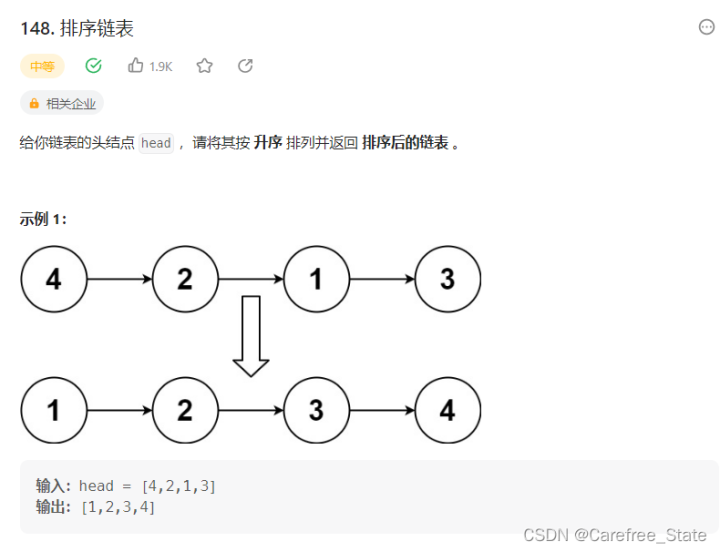
7.3.1选择排序链表

用选择排序的方式去排序链表，缺点就是代码复杂，有很多要考虑的

并且速度慢，力扣跑不过，时间复杂度达到N2

publicListNodesortList(ListNodehead){intcount=0;if(head==null){returnnull;}ListNoderet=head;ListNodeprevHead=null;while(head!=null){ListNodemaxNode=head;ListNodecur=head;ListNodeprev=head;while(cur!=null){if(cur.next!=null&&cur.next.val>maxNode.val){prev=cur;maxNode=cur.next;}cur=cur.next;}if(count==0){prevHead=maxNode;count++;}if(maxNode==ret){head=head.next;continue;}if(maxNode==head){prev=prevHead;head=head.next;}ListNodelinker=maxNode;prev.next=maxNode.next;linker.next=ret;ret=linker;}returnret;}

五万个数据，这种排序太慢了！

这里不做重点讲解，思路就是从后面选择一个最大的头插过去，重点也是要记住最大的最大的那个[尾结点]

7.3.2递归排序链表

时间复杂度O(N*log2N),空间复杂度O(1)；

思路跟刚才归并怎么排一致，重点在于用快慢指针找到中点，节省速度

是可以先求长度然后一直用的（就是算一次长度，然后每次都用这个长度为基准，去找mid）

之后不断合并有序链表。

再看一次动图吧：

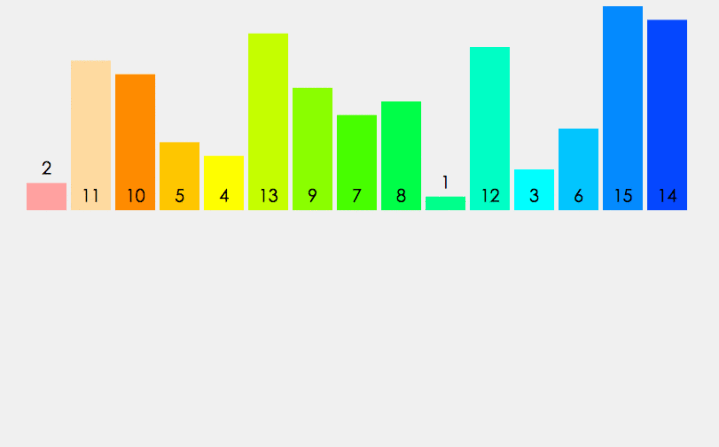
递归的重点就分清“整体感”，比如说下面的，我们就看做左右边已经弄好了，只要满足小问题（递归出口

），通过数学归纳法就能知道成立

ListNodeleft=sortList(head);ListNoderight=sortList(tmp);publicListNodesortList(ListNodehead){if(head==null