[Java高阶数据结构]图-图的表示与遍历

Java高阶数据结构&图的概念&图的存储与遍历

1.图的基本概念

1.1图的属性

图是由顶点集合及顶点间的关系组成的一种数据结构：

G=(V，E)

Graph图，vertex顶点，edge边

其中：顶点集合V={x|x属于某个数据对象集}是有穷非空集合；

E={(x,y)|x,y属于V}或者E={|x,y属于V&&Path(x,y)}，是顶点间关系的有穷集合，也叫做边的集合。

(x,y)表示x到y的一条双向通路，即边(x,y)是无方向的；

Path表示从x到y的一条单向通路，即Path(x,y)是有方向的。

顶点和边：

图中结点称为顶点，

第i个顶点记作vi。

两个顶点vi和vj相关联称作顶点vi和顶点vj之间有一条边，

图中的第k条边记作ek，ek=无向边(vi，vj)或有向边Path（vi，vj）

1.2无向图与有向图

在有向图中，顶点对是有序的，顶点对称为顶点x到顶点y的一条边(弧)，Path(x,y)和Path(y,x)是两条不同的边，比如下图G3和G4为有向图。

在无向图中，顶点对(x,y)是无序的，顶点对(x,y)称为顶点x和顶点y相关联的一条边，这条边没有特定方向，Path(x,y)和Path(y,x)是同一条边，比如下图G1和G2为无向图。

注意：无向边(x,y)等于有向边Path(x,y)和Path(y,x)

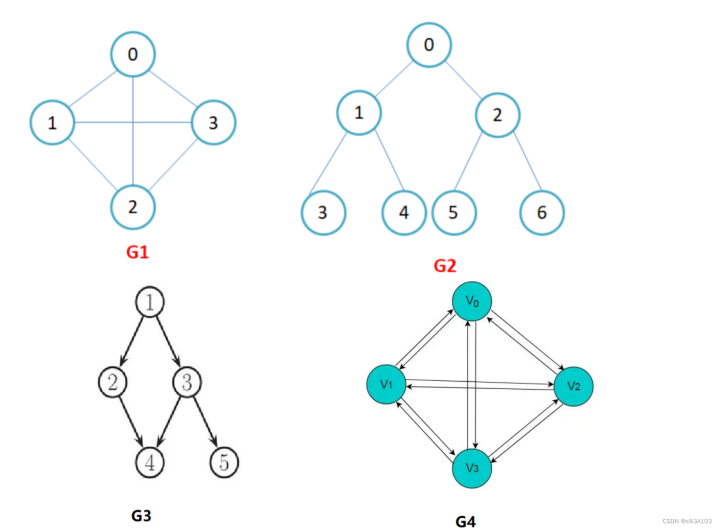
在有n个顶点的

无向图中，n(n-1)/2条边

任何两个顶点都有且仅有一条边

根据排列组合原理，第一个顶点可连接n-1个顶点,第二个顶点可以连接n-2个顶点······

第n个顶点可连接0个顶点，总和n(n-1)/2

[------]

即无向完全图，如G1

有向图中，n(n-1)条边

任何两个顶点都有且仅有两条方向相反的边

n(n-1)/2*2=n(n-1)

[]

即有向完全图，如G4

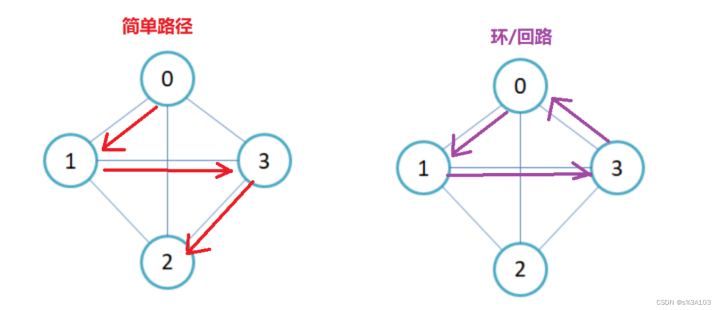
1.4简单路径和回路

简单路径：路径上的顶点（V1，V2······）均不重复

回路：若路径上的第一个顶点与最后一个顶点重合，即成环回路

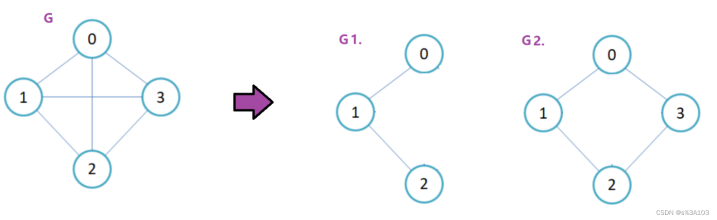
即图G集合的子集G1={V1,E1},则称G1为G的子图

V1包含于V

E1包含于E

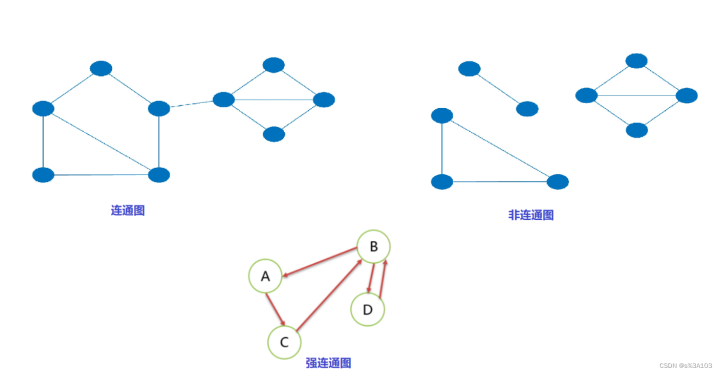
无向图中，V1到V2有路径，则称V1和V2连通

如果每对顶点都是连通的，则称此图为连通图

如果此图为有向图，并且每一对顶点Vi到Vj与Vj到Vi都连通，则称为强连通图

完全图就是更加强大的连通图~

生成树在求最小生成树篇章讲解

2.图的存储（理论）

2.1※邻接矩阵

如果一个图，有n个顶点（V0···Vn-1）

每个顶点都有对应的下标（0···n-1）

那么邻接矩阵就是个n×n的矩阵

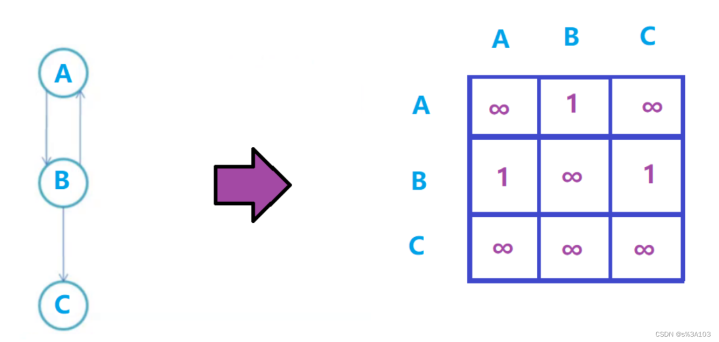
如果顶点Vi到Vj有一条有向边---->

直接相连

那么这个矩阵（二维数组）的的i行第j列的元素置为对应的距离（权值）

带权图（不带权图默认为1）

默认值为∞（无穷大）

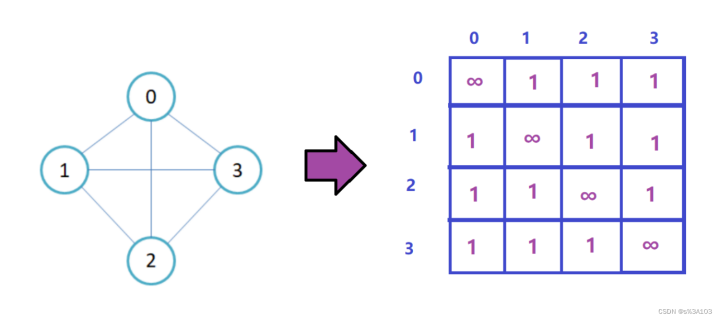
无向图的一条边是双向的

自己到自己可以是0也可以是默认值∞，最好是∞，这样后面好判断

无向图的邻接矩阵是关于对角线对称的：

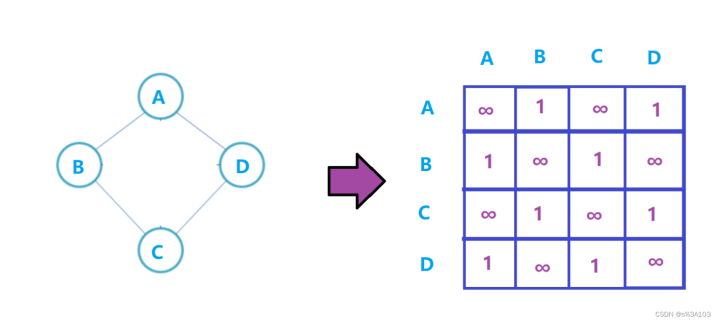
有向图则不一定：

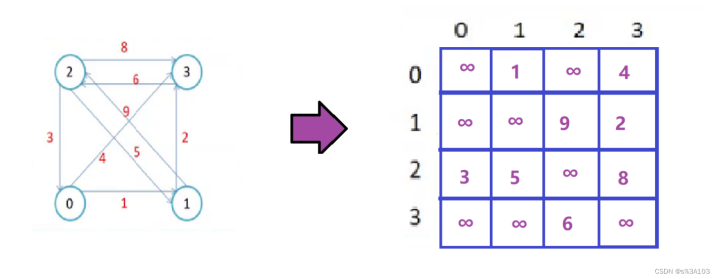
带权图：

2.2邻接链表

邻接表：

用数组表示顶点的集合

用链表来表示边的关系

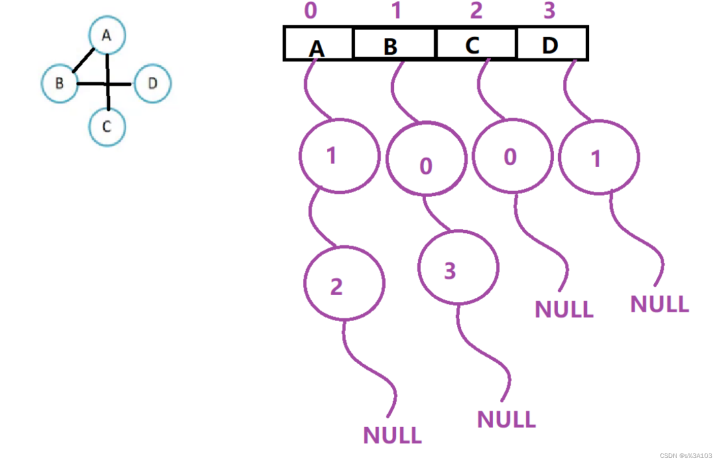
解析：

A可以到B和C，则A对应的链表存放两个节点[1->2->null]

B可以到A和D，则B对应的链表存放两个节点[0->3->null]

C可以到A，则C对应的链表存放一个节点[0->null]

D可以到B，则D对应的链表存放一个节点[1->null]

如果是有向图的邻接表，则分为两种

入边表

出边表

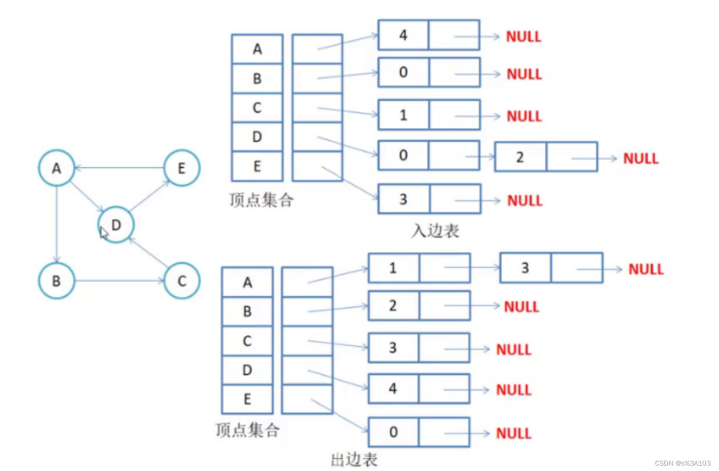
那么所有的链表的节点和就是边数

因为一条有向边必然是一个顶点的“出”，另一个顶点的“入”

3.图的存储（代码表示）

3.1邻接矩阵

3.1.1邻接矩阵的基本属性

publicclassGraphByMatrix{//1.顶点集合privatechar[]arrayV;//2.邻接矩阵privateint[][]matrix;//顶点在这里的下标即在字符数组的下标//3.是否是有向图privatebooleanisDirect;}

3.1.2构造方法和初始化方法

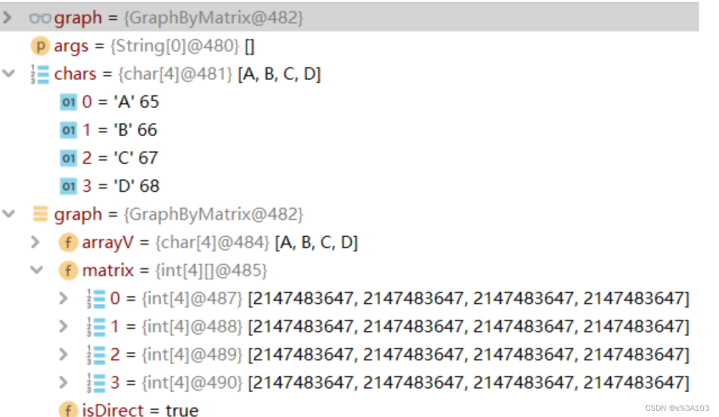
/****@paramsize[顶点个数]*@paramisDirect*/publicGraphByMatrix(intsize,booleanisDirect){this.arrayV=newchar[size];matrix=newint[size][size];//此时默认都是0this.isDirect=isDirect;//将邻接矩阵默认值改为[∞]for(inti=0;i

构造方法

传入size，即顶点的个数==>arrayV的大小

传入isDirect，即确认是有向图或者无向图

将邻接矩阵的默认值改为无穷大

初始化顶点集合

传入字符数组，挨个赋值

测试：

publicstaticvoidmain(String[]args){char[]chars={'A','B','C','D'};GraphByMatrixgraph=newGraphByMatrix(chars.length,true);graph.initArrayV(chars);System.out.println;}

3.1.3获取顶点字符在顶点集合中的下标

这个方法获得的下标，也代表该顶点在邻接矩阵的下标

可以用哈希表去存储顶点们，这里不是~

所以我用的是遍历数组的方法

//获得顶点对应下标publicintgetIndexOfV(charv){for(inti=0;i

3.1.4增加边

参数左指向参数右的有向边

如果是无向图，默认参数右也指向参数左

/***添加边*@paramv1起始顶点*@paramv2目的顶点*@paramweight权值*/publicvoidaddEdge(charv1,charv2,intweight){intindex1=getIndexOfV(v1);intindex2=getIndexOfV(v2);if(index1!=-1&&index2!=-1&&index1!=index2){matrix[index1][index2]=weight;//index1-->index2if(!isDirect){//无向图matrix[index2][index1]=weight;}}}

测试：

publicstaticvoidmain(String[]args){char[]chars={'A','B','C','D'};GraphByMatrixgraph=newGraphByMatrix(chars.length,true);graph.initArrayV(chars);graph.addEdge('A','B',1);graph.addEdge('A','D',1);graph.addEdge('B','A',1);graph.addEdge('B','C',1);graph.addEdge('C','B',1);graph.addEdge('C','D',1);graph.addEdge('D','A',1);graph.addEdge('D','C',1);System.out.println;}}

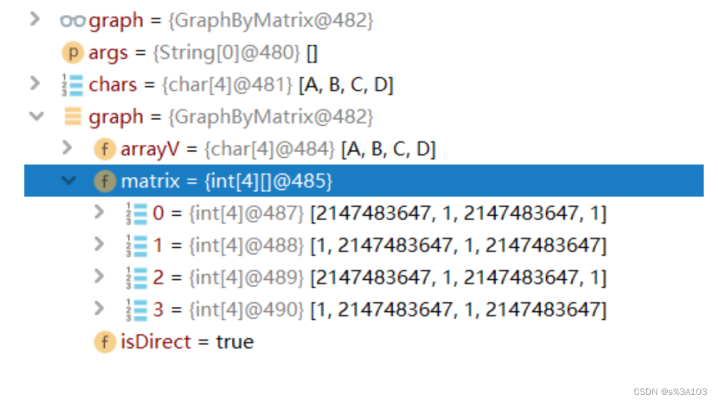
对比：

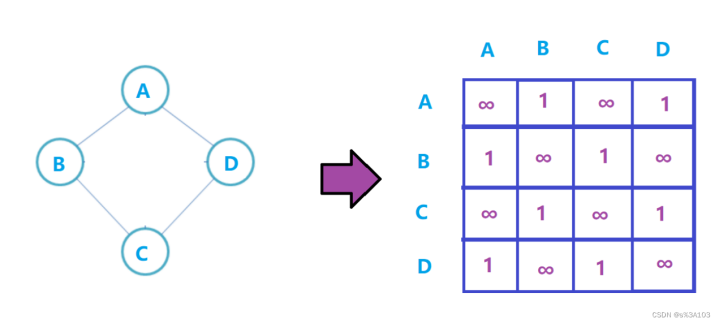
3.1.5打印邻接矩阵

//打印邻接矩阵publicvoidprintGraph{System.out.print("");for(inti=0;i

测试：

graph.printGraph;

3.1.6获得顶点的度

什么是顶点的度？

有向图，入顶点和出顶点的边数和

无向图，与顶点相连的边的数量

则对于无向图，只需要遍历一行就行，但是对于有向图，还需要遍历对应列

//获得顶点的度publicintgetDevOfV(charv){intindexV=getIndexOfV(v);intcount=0;//无论如何，都要遍历对于行for(inti=0;i

测试：

if(graph.isDirect){System.out.println("有向图：");}else{System.out.println("无向图：");}System.out.println("A节点的度："+graph.getDevOfV('A'));System.out.println("B节点的度："+graph.getDevOfV('B'));System.out.println("C节点的度："+graph.getDevOfV('C'));System.out.println("D节点的度："+graph.getDevOfV('D'));

3.2邻接链表

3.2.1邻接链表的基本属性

publicclassGraphByList{staticclassNode{publicintsrc;//起始下标publicintdest;//目的下标publicintweigh;//权值publicNodenext;//后继publicNode(intsrc,intdest,intweigh){this.src=src;this.dest=dest;this.weigh=weigh;}}publicchar[]arrayV;//顶点集合publicArrayListedgeList;//边的集合publicbooleanisDirect;//是否是有向图}

定义内部类节点Node

顶点集合arrayV

边集合edgeList

也可以用数组

标识符isDirect去区分有向图和无向图

如果是

出边邻接表，边集合中第i条链表上的节点的src成员都是i值

入边邻接表，边集合中第i条链表上的节点的dest成员都是i值

3.2.2构造方法和初始化方法

publicGraphByList(intsize,booleanisDirect){this.arrayV=newchar[size];edgeList=newArrayList(size);//不带参数的话，默认大小为0//并且，这只是他的容量是sizefor(inti=0;i

构造方法

传入size，顶点集合和边集合的大小

传入isDirect，确定有向或者无向

初始化方法

对顶点集合挨个赋值

3.2.3获取顶点字符在顶点集合的下标

这里获得的下标，就是该顶点在边集合里对应的下标

依旧使用的是遍历数组的方法

//获得顶点对应下标publicintgetIndexOfV(charv){for(inti=0;i

3.2.4添加边

参数左指向参数右的有向边

这是出边表，入边表相反，本文章只写出边表

如果是无向图，默认参数右也指向参数左

注意：重复输入同一条有向边，一定要排除

/***添加边*这里写的是[出边表]*[入边表]就是倒过来*@paramv1起始顶点*@paramv2目的顶点*@paramweight权值*/publicvoidaddEdge(charv1,charv2,intweight){intindex1=getIndexOfV(v1);intindex2=getIndexOfV(v2);if(index1!=-1&&index2!=-1&&index1!=index2){Nodecur=edgeList.get(index1);//判断是否存在此边while(cur!=null){if(cur.dest==index2){System.out.println("存在此边");return;}cur=cur.next;}NodenewOne=newNode(index1,index2,weight);//[index1-->index2]//头插法插入节点newOne.next=edgeList.get(index1);edgeList.set(index1,newOne);//如果是无向图，相反的边也一并添加//如果是无向图，添加操作是联动的，所以上面判断不存在此边//此时不用判断if(!isDirect){Nodenode=newNode(index2,index1,weight);//[index2-->index1]node.next=edgeList.get(index2);edgeList.set(index2,node);}}}

测试：

publicstaticvoidmain(String[]args){char[]chars={'A','B','C','D'};GraphByListgraph=newGraphByList(chars.length,true);graph.initArrayV(chars);graph.addEdge('A','B',1);graph.addEdge('A','D',1);graph.addEdge('B','A',1);graph.addEdge('B','C',1);graph.addEdge('C','B',1);graph.addEdge('C','D',1);graph.addEdge('D','A',1);graph.addEdge('D','C',1);System.out.println;}

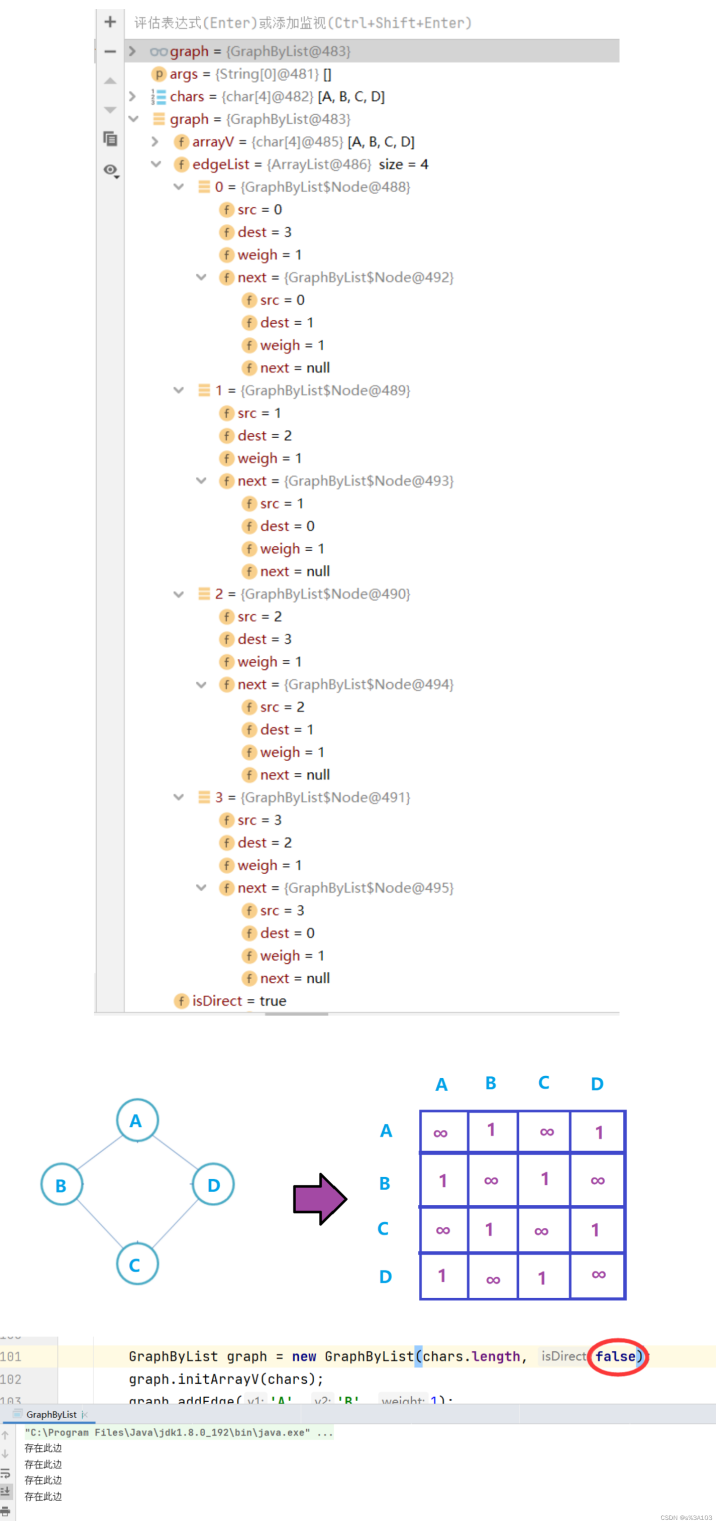
3.2.5打印的邻接链表

//打印邻接表publicvoidprintGraph{for(inti=0;i"+arrayV[index2]+"]");cur=cur.next;}System.out.println;}}

获取对应下标的链表

遍历链表

测试：

graph.printGraph;

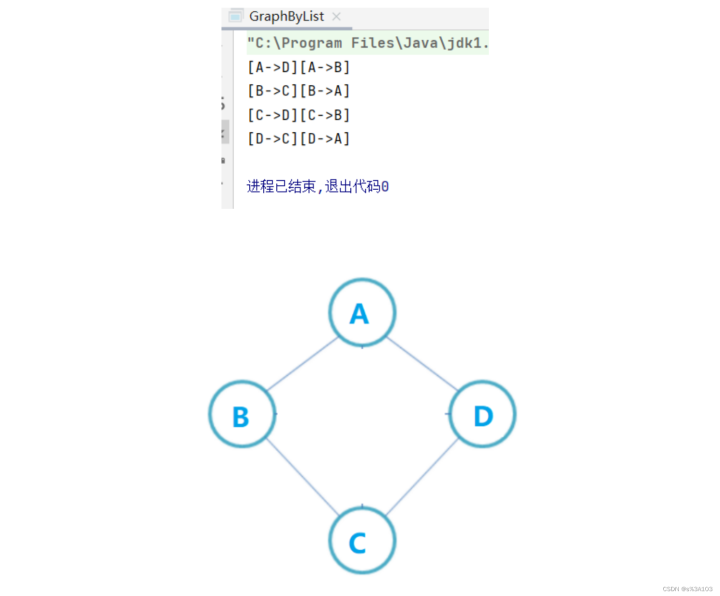
3.2.6获得顶点的度

有向图，入顶点和出顶点的边数和

无向图，与顶点相连的边的数量

对应邻接链表

有向图：

入边表的对应链表的长度+出边表对应链表的长度

但是我们的表是出边表,所以要遍历其他下标的链表，获得入边的数量

无向图：

对应链表的长度，就是度数~

注意：入边表和出边表只要一种就可以完整的图了，并不是入边表和出边表结合去代表！

//获得顶点的度publicintgetDevOfV(charv){intindex=getIndexOfV(v);intcount=0;if(index!=-1){Nodecur=edgeList.get(index);while(cur!=null){count++;cur=cur.next;}//如果是有向图if(isDirect){intdest=index;for(intsrc=0;src

测试：

System.out.println("A节点的度："+graph.getDevOfV('A'));System.out.println("B节点的度："+graph.getDevOfV('B'));System.out.println("C节点的度："+graph.getDevOfV('C'));System.out.println("D节点的度："+graph.getDevOfV('D'));

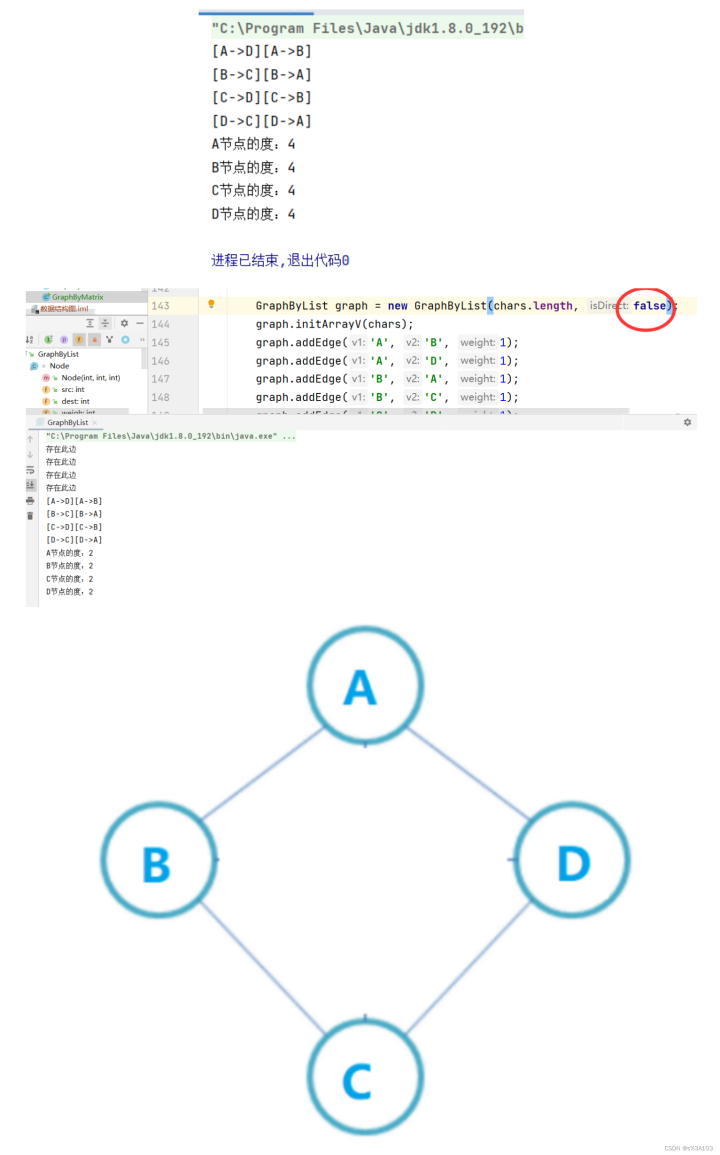
4.图的遍历

这里只讲解邻接矩阵的遍历代码~

感兴趣的同学可以去研究一下邻接表的遍历

这里用到的邻接矩阵的图对象就是上面定义的！

4.1广度优先的遍历

类似于树的层序遍历

树就是特殊的图罢了

优先打印此顶点直接相连的所有顶点

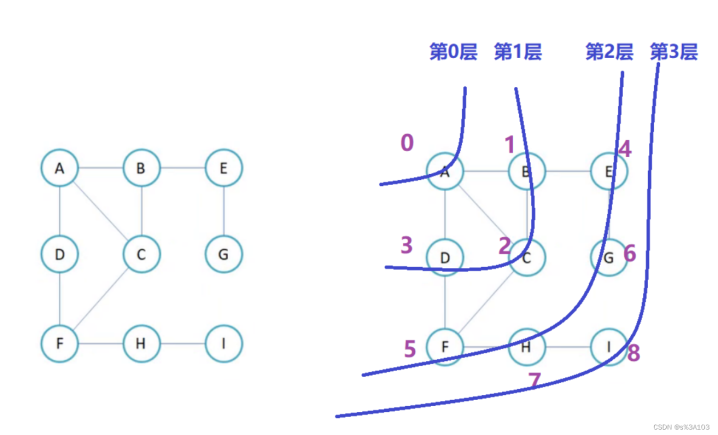
算法设计一样也是非递归，利用队列

打印过的不用再打印，所以需要一个数组来标记每个顶点的是否被打印过

否则会死循环

BreadthFirstSearch,广度优先遍历

//广度优先遍历publicvoidbfs(charv){//标记数组boolean[]isVisited=newboolean[arrayV.length];//定义一个队列Queuequeue=newLinkedList;//获取起始顶点的下标intindex=getIndexOfV(v);if(index==-1){return;}queue.offer(index);while(!queue.isEmpty){inttop=queue.poll;isVisited[top]=true;System.out.print(arrayV[top]+"");for(inti=0;i

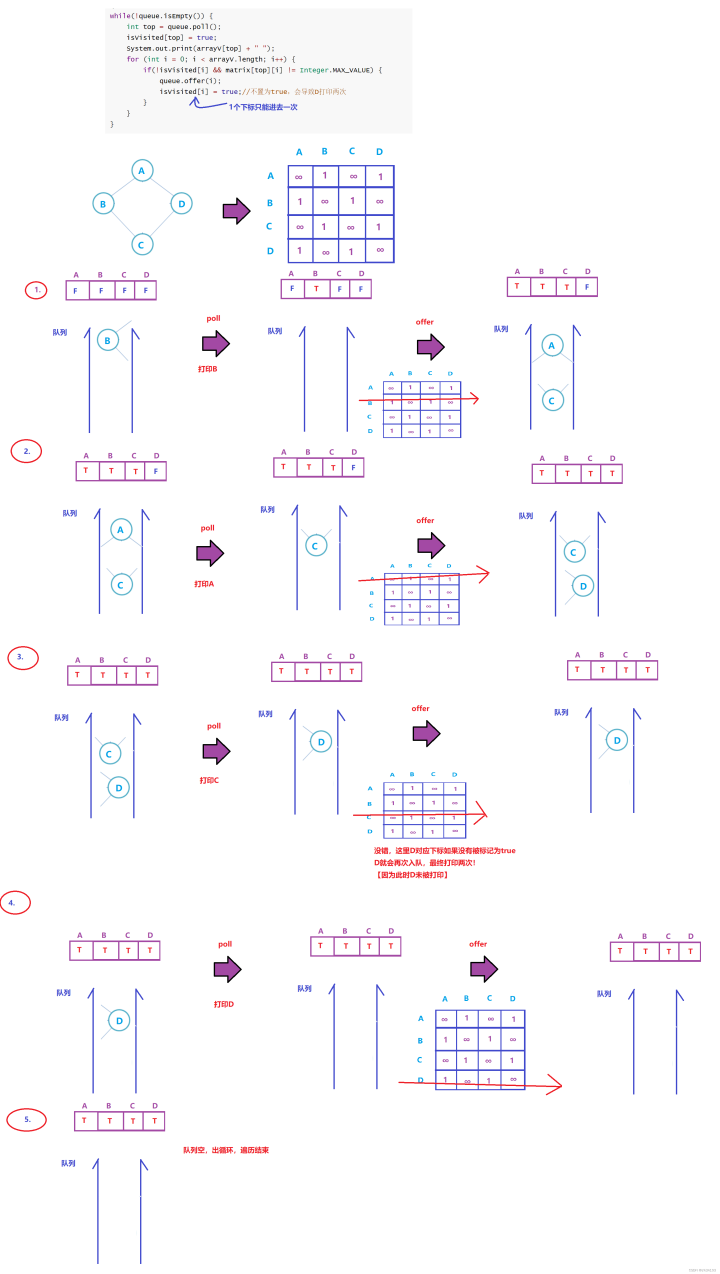
可能有人用count，去计算打印了多少个顶点，打印到对应数量就出循环

发现入队列的时候不置为true也能正确~

这只是巧合！更复杂的图就不会这么巧了，会因为你重复打印而误判为已全部打印

测试：

graph.bfs('B');

4.2深度优先的遍历

类似于树的先序遍历

树就是特殊的图罢了

尽可能的深入到与实时顶点相连的顶点，直到实时顶点不能再深入到未打印的顶点，再回溯

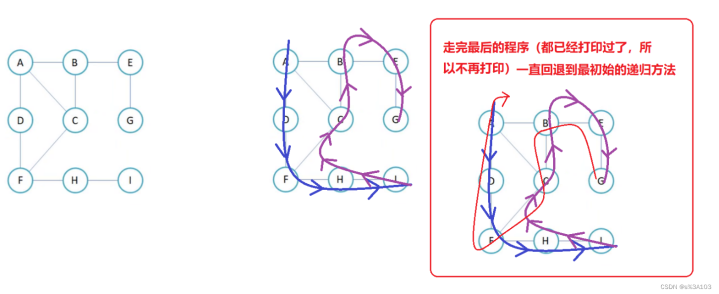
DepthFirstSearch,深度优先遍历

算法设计，一样可以递归也可以非递归（栈）

这里这写递归的写法~

打印过的不用再打印，所以需要一个数组来标记每个顶点的是否被打印过

否则会死递归

//深度优先遍历publicvoiddfs(charv){boolean[]isVisited=newboolean[arrayV.length];intsrc=getIndexOfV(v);dfsOrder(src,isVisited);}//递归方法privatevoiddfsOrder(intsrc,boolean[]isVisited){System.out.print(arrayV[src]+"");isVisited[src]=true;for(inti=0;i

用树/递归的整体化思想就能解决了，我们是类似先序遍历，先打印顶点的~

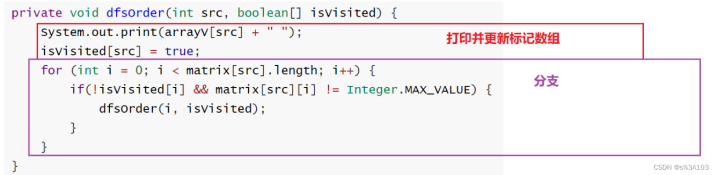
不一样的是，这里的递归出口就是顶点无法继续深入到未打印的顶点

有人会问了，这里需要进入递归前就置为true吗，跟刚才那个一样

答：不用

因为递归不像刚才那个，刚才那个打印是延时打印的，也就是说放在队列里面，慢慢按顺序打印

所以

bfs时，会出现延时打印而重复入队的现象。

dfs则不一样，没有延时打印，一进递归就打印和更新，下次要进递归之前会判断该下标是否被打印过

测试：

graph.dfs('B');

对于非连通图的遍历，一次遍历如果不能打印所有顶点，那么只需要用别的顶点去遍历，（由于有标记的顶点不会被再次打印），直到把所有顶点打印！

最坏的情况就是，所有的顶点这间一条边都没有，那么以每个顶点为起始顶点打印一次，也能打印全部顶点